Saccheri quadrilateral

A Saccheri quadrilateral is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his 1733 book Euclides ab omni naevo vindicatus (Euclid freed of every flaw), an attempt to prove the parallel postulate using the method reductio ad absurdum. Such a quadrilateral is sometimes called a Khayyam–Saccheri quadrilateral to credit Persian scholar Omar Khayyam who described it in his 11th century book Risāla fī šarḥ mā aškala min muṣādarāt kitāb Uqlīdis (Explanations of the difficulties in the postulates of Euclid).^[1]

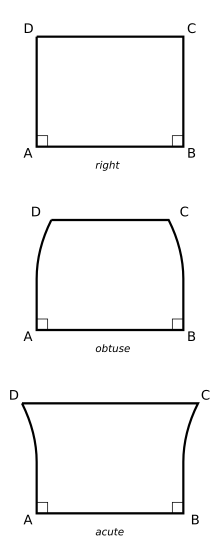
For a Saccheri quadrilateral ${\displaystyle ABCD,}$ the legs ${\displaystyle AD}$ and ${\displaystyle BC}$ are equal in length and each perpendicular to the base ${\displaystyle AB.}$ The top ${\displaystyle CD}$ is called the summit and the angles at ${\displaystyle C}$ and ${\displaystyle D}$ are called the summit angles.

The advantage of using Saccheri quadrilaterals when considering the parallel postulate is that they clearly present three mutually exclusive options: Are the summit angles right angles, obtuse angles, or acute angles?

Saccheri himself did not consider the possibility of non-Euclidean geometry and believed that both the obtuse and acute cases could be shown to be contradictory from Euclid's other postulates. He did show that the obtuse case was contradictory, but failed to properly handle the acute case.^[2]

The existence of a Saccheri quadrilateral with right angles at the summit for any base and sides is equivalent to the parallel postulate, leading to Euclidean geometry. In hyperbolic geometry, arising from the negation of the parallel postulate, the summit angles are always acute. In elliptic or spherical geometry (which require a few modifications to Euclid's other postulates),^[3] the summit angles are always obtuse.