Back امتداد تحليلي Arabic Continuació analítica Catalan Analytische Fortsetzung German Analytic continuation English Extensión analítica Spanish ادامه تحلیلی FA Prolongamento analítico GL המשכה אנליטית HE Անալիտիկ շարունակություն HY Prolungamento analitico Italian
Cet article est une ébauche concernant l’analyse.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
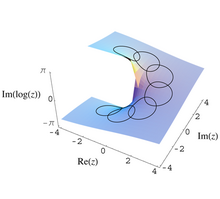
En analyse complexe, la théorie du prolongement analytique détaille l'ensemble des propriétés et techniques relatives au prolongement des fonctions holomorphes (ou analytiques). Elle considère d'abord la question du prolongement dans le plan complexe. Puis elle aborde des formes plus générales d'extension qui permettent de prendre en compte les singularités et les complications topologiques qui les accompagnent. La théorie fait alors intervenir soit le concept assez ancien et peu opérant de fonction multiforme, soit le concept plus puissant de surface de Riemann.
Il existe également une théorie du prolongement analytique pour les fonctions de plusieurs variables complexes, dont la difficulté est plus grande, et dont le traitement fut à l'origine de l'introduction de la cohomologie des faisceaux.