Leis de De Morgan

En lóxica proposicional e álxebra de Boole, as leis de De Morgan,^[1][2][3] tamén coñecidas como teorema de De Morgan,^[4] son un par de regras de transformación que son regras de inferencia válidas. Levan o nome de Augustus De Morgan, un matemático británico do século XIX. As regras permiten a expresión de conxuncións e disxuncións unicamente en termos entre si mediante a negación.

As regras pódense expresar en texto como:

• A negación de "A e B" é o mesmo que "non A ou non B".
• A negación de "A ou B" é o mesmo que "non A e non B".

ou

• O complementario da unión de dous conxuntos é o mesmo que a intersección dos seus complementos
• O complementario da intersección de dous conxuntos é o mesmo que a unión dos seus complementarios

ou

• non (A ou B) = (non A) e (non B)
• non (A e B) = (non A) ou (non B)

onde "A ou B" é "ou inclusivo" que significa polo menos un de A ou B en lugar de "ou exclusivo" que significa exactamente un de A ou B.

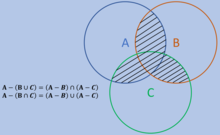
Outra forma da lei de De Morgan é a seguinte como se ve a continuación.

${\displaystyle A-(B\cup C)=(A-B)\cap (A-C),}$

${\displaystyle A-(B\cap C)=(A-B)\cup (A-C).}$

A aplicación destas regras inclúen a simplificación de expresións lóxicas en programas informáticos e deseños de circuítos dixitais. As leis de De Morgan son un exemplo dun concepto máis xeral de dualidade matemática.

1. ↑ Copi, Irving M.; Cohen, Carl; McMahon, Kenneth (2016). Introduction to Logic. ISBN 9781315510880. doi:10.4324/9781315510897. 
2. ↑ Hurley, Patrick J. (2015). A Concise Introduction to Logic (12th ed.). Cengage Learning. ISBN 978-1-285-19654-1. 
3. ↑ Moore, Brooke Noel (2012). Critical thinking. Richard Parker (10th ed.). New York: McGraw-Hill. ISBN 978-0-07-803828-0. OCLC 689858599. 
4. ↑ DeMorgan's [sic] Theorem