Pengguna:Dedhert.Jr/Uji halaman 02.1

Bilangan prima Mersenne dan bilangan sempurna adalah jenis bilangan asli yang sangat terkait erat dalam teori bilangan. Bilangan prima Mersenne, dinamai dari Marin Mersenne, adalah bilangan prima yang dapat ditulis sebagai 2^p − 1 untuk suatu bilangan bulat positif p. Sebagai contoh, 3 adalah bilangan prima Mersenne sebab ia adalah bilangan prima dan dapat ditulis sebagai 2² − 1.^[1][2] Bilangan p yang bersesuaian dengan bilangan prima Mersenne harus merupakan bilangan prima, walaupun tidak semua p menghasilkan bilangan prima Mersenne; sebagai contoh, 2¹¹ − 1 = 2047 = 23 × 89.^[3] Sementara itu, bilangan sempurna adalah bilangan asli yang sama dengan jumlah dari faktor-faktornya kecuali bilangan itu sendiri. Sebagai contoh, 6 adalah bilangan sempurna sebab faktor dari 6 adalah 1, 2, dan 3, serta 1 + 2 + 3 = 6.^[2][4]

Terdapat korespondensi satu-satu di antara bilangan prima Mersenne dan bilangan sempurna genap. Menurut teorema Euklides–Euler, teorema yang dibuktikan sebagian oleh Euklides dan kemudian diselesaikan oleh Leonhard Euler, bilangan genap adalah sempurna jika dan hanya jika bilangan tersebut dapat ditulis sebagai 2^{p − 1} × (2^p − 1), dengan 2^p − 1 adalah bilangan prima Mersenne. Dengan kata lain, semua bilangan yang disubstitusikan ke ekspresi tersebut dikatakan sempurna, terutama semua bilangan sempurna genap. Sebagai contoh, untuk kasus p = 2, maka 2² − 1 = 3 adalah bilangan prima, dan 2^{2 − 1} × (2² − 1) = 2 × 3 = 6 adalah bilangan sempurna.^[1][5][6]

Saat ini, terdapat masalah terbuka yang menanyakan adakah tak berhingga banyaknya bilangan prima Mersenne dan bilangan sempurna genap.^[2][6] Bilangan prima Mersenne seringkali dikaitkan dengan konjektur Lenstra–Pomerance–Wagstaff, konjektur yang menyatakan bahwa jumlah bilangan prima yang lebih kecil daripada suatu x kira-kira sama dengan (e^γ / log 2) × log log x, dengan e adalah bilangan yang kira-kira sama dengan 2,7182818..., γ adalah konstanta Euler–Mascheroni, dan log adalah logaritma alami.^[7][8][9] Selain itu, masih belum diketahui jika sebarang bilangan sempurna ganjil itu ada; berbagai syarat mengenai bilangan sempurna ganjil yang mungkin sudah dibuktikan, terutama bilangan yang lebih besar daripada 10¹⁵⁰⁰.^[10]

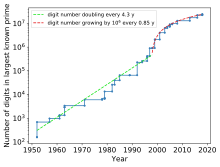
Berikut adalah daftar bilangan prima Mersenn dan bilangan sempurna yang diketahui saat ini, beserta dengan pangkat p. Hingga 2022^[update], terdapat 51 bilangan prima Mersenne yang diketahui (dan juga bilangan sempurna); 17 bilangan prima Mersenne dan bilangan sempurna terbesar telah ditemukan menggunakan proyek komputasi terdistribusi Great Internet Mersenne Prime Search (GIMPS).^[2] Bilangan prima Mersenne yang baru telah ditemukan menggunakan uji Lucas–Lehmer, suatu uji primalitas bilangan prima Mersenne yang sangat mudah digunakan untuk komputer biner.^[2]

The displayed ranks are among indices currently known hingga 2022^[update]; while unlikely, ranks may change if smaller ones are discovered. According to GIMPS, all possibilities less than the 48th working exponent p = 57,885,161 have been checked and verified hingga Oktober 2021^[update].^[11] The discovery year and discoverer are of the Mersenne prime, since the perfect number immediately follows by the Euclid–Euler theorem. Discoverers denoted as "GIMPS / name" refer to GIMPS discoveries with hardware used by that person. Later entries are extremely long, so only the first and last 6 digits of each number are shown.

1. ^ ^{a b} Kesalahan pengutipan: Tag <ref> tidak sah; tidak ditemukan teks untuk ref bernama stillwell
2. ^ ^{a b c d e} Kesalahan pengutipan: Tag <ref> tidak sah; tidak ditemukan teks untuk ref bernama caldwellmp
3. ^ Kesalahan pengutipan: Tag <ref> tidak sah; tidak ditemukan teks untuk ref bernama caldwell
4. ^ Kesalahan pengutipan: Tag <ref> tidak sah; tidak ditemukan teks untuk ref bernama prielipp
5. ^ Kesalahan pengutipan: Tag <ref> tidak sah; tidak ditemukan teks untuk ref bernama caldwellepn
6. ^ ^{a b} Kesalahan pengutipan: Tag <ref> tidak sah; tidak ditemukan teks untuk ref bernama crilly2007
7. ^ Kesalahan pengutipan: Tag <ref> tidak sah; tidak ditemukan teks untuk ref bernama caldwelllpw
8. ^ Kesalahan pengutipan: Tag <ref> tidak sah; tidak ditemukan teks untuk ref bernama wagstaff
9. ^ Kesalahan pengutipan: Tag <ref> tidak sah; tidak ditemukan teks untuk ref bernama pomerance
10. ^ Kesalahan pengutipan: Tag <ref> tidak sah; tidak ditemukan teks untuk ref bernama ochem
11. ^ "GIMPS Milestones Report". Great Internet Mersenne Prime Search. Diarsipkan dari versi asli tanggal 13 October 2021. Diakses tanggal 7 January 2022.  Parameter |url-status= yang tidak diketahui akan diabaikan (bantuan)