Integral

Eit integral av ein matematisk funksjon er i differensialrekning ei utviding av konseptet summasjon. Prosessen med å finne integral vert kalla integrasjon eller integrering, og vert vanlegvis brukt for å finne totalsummen av eigenskapar som areal, volum, masse, forskyving osv, når fordelinga eller endringsraten med omsyn til andre storleikar (posisjon, tid) er spesifisert. Det finst fleire forskjellige definisjonar på integrasjon som inneber forskjellige tekniske metodar. Dei er derimot samsvarande, og to forskjellige måtar å integrere ein funksjon på vil gje same resultat når begge er definert.

Uttrykket «integral» kan òg referere til antideriverte. Sjølv om dei er nært knytt saman gjennom analysen sitt fundamentalteorem, er dei to førestillingane omgrepsmessig forskjellige. Ein antiderivert vert ofte referert til som eit ubestemt integral (ein funksjon), medan integral i denne artikkelen omhandlar bestemte integral.

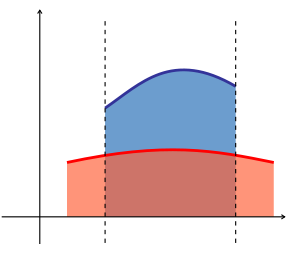
Integralet til ein funksjon f med ein reell variabel x på intervallet [a, b] er lik arealet mellom linjene x = a, x = b, x-aksen, og kurva som vert definert av grafen til f. Dette vert formalistert av den enklaste forma av eit integral, Riemann-integralet, som gjev oss ein metode for å rekne ut dette arealet ved å bruke grenser for å dele arealet inn i tynnare rektangulære striper og føreta summen av arealet til kvar stripe. (sjå døme på dette).

Eit alternativ er å la

${\displaystyle S=\{(x,y)\in \mathbb {R} ^{2}:a\leq x\leq b,0\leq y\leq f(x)\},}$

slik at integralet av f mellom a og b er eit mål av S. I denne metoden gjev integrasjon eit tal knytt til S, som gjev oss ein ide om «storleiken» til settet (men dette er forskjellig frå kardinalitet eller storleiksorden). Dette fører til ein annan og meir mektig definisjon av integralet, kalla Lebesgue-integral.

Leibniz introduserte lang s som notasjon for integralet. Integralet diskutert over ville då ha vore skrive ${\displaystyle \int _{a}^{b}f(x)\,dx}$. ${\displaystyle \int _{\,}^{\,}}$-teiknet representerer integrasjonen, a og b er grenseverdiane i intervallet, f(x)' er funksjonen som vert integrert, kalla integrand, og dx er notasjonen for integrasjonsvariabelen. Historisk sett representerte dx ein infinitesimal storleik, og lang s stod for «sum». I moderne integrasjonsteoriar, som er bygd opp på andre grunnlag, vert ikkje denne notasjonen lenger tenkt på som ein sum, bortsett frå i dei mest uformelle tilfella. I dag representerer dx eit differensial.

Viss f til dømes er ein konstant funksjon f(x) = 3, så vil integralet av f mellom 0 og 10 vere arealet av rektangelet som er avgrensa av linjene x = 0, x = 10, y = 0, og y = 3. Arealet til dette rektangelet er breidda multiplisert med høgda, så verdien av integralet er 30. Det same resultatet vil ein finne ved å integrere funksjonen, men metoden vert vanlegvis brukt for meir kompliserte eller glatte kurver.