Matematisk induktion

Den här artikeln behöver källhänvisningar för att kunna verifieras. (2018-12) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan.

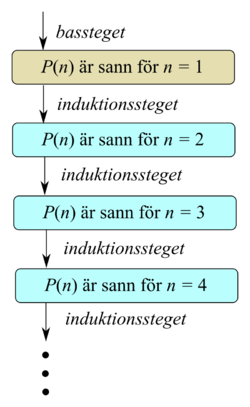
Matematisk induktion är en bevismetod som tillämpas på påståenden som omfattar mängden av naturliga tal som är större än eller lika med ett startvärde (till exempel 0 eller 1)^[1]. Då mängden naturliga tal är obegränsad kan bevis inte utföras för varje enskilt fall. I det generella induktionsbeviset delas beviset för påståendet upp i tre steg:

• Induktionsbasen: först visas att påståendet är sant för ett startvärde, till exempel för heltalet n = 1
• Induktionsantagandet: utsagan antas vara sann för något heltal n
• Induktionssteget: visa att om induktionsantagandet är sant, så är påståendet också sant för n + 1

När dessa steg är utförda är det bevisat att påståendet gäller för alla n från och med det antagna startvärdet. Tekniken kan även tillämpas på de matematiska objekt som är vidareutvecklingar av de positiva heltalen, ordinaltalen.

Denna bevismetod är av grundläggande betydelse för aritmetik och mängdlära och därmed för alla områden av matematiken.

Tekniken kan illustreras med dominobrickor: varje dominobricka är ställd på högkant och representerar ett tal i den ordnade följden av positiva heltal. Om en bricka välter, välter den också den nästföljande brickan. Induktionsprincipen innebär att samtliga dominobrickor kommer att bli välta om den första brickan har blivit vält.