Homothety

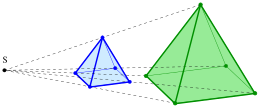
In mathematics, a homothety (or homothecy, or homogeneous dilation) is a transformation of an affine space determined by a point S called its center and a nonzero number ${\displaystyle k}$ called its ratio, which sends point ${\displaystyle X}$ to a point ${\displaystyle X'}$ by the rule ^[1]

${\displaystyle {\overrightarrow {SX'}}=k{\overrightarrow {SX}}}$ for a fixed number ${\displaystyle k\neq 0}$.

Using position vectors:

${\displaystyle \mathbf {x} '=\mathbf {s} +k(\mathbf {x} -\mathbf {s} )}$.

In case of ${\displaystyle S=O}$ (Origin):

${\displaystyle \mathbf {x} '=k\mathbf {x} }$,

which is a uniform scaling and shows the meaning of special choices for ${\displaystyle k}$:

for ${\displaystyle k=1}$ one gets the identity mapping,

for ${\displaystyle k=-1}$ one gets the reflection at the center,

For ${\displaystyle 1/k}$ one gets the inverse mapping defined by ${\displaystyle k}$.

In Euclidean geometry homotheties are the similarities that fix a point and either preserve (if ${\displaystyle k>0}$) or reverse (if ${\displaystyle k<0}$) the direction of all vectors. Together with the translations, all homotheties of an affine (or Euclidean) space form a group, the group of dilations or homothety-translations. These are precisely the affine transformations with the property that the image of every line g is a line parallel to g.

In projective geometry, a homothetic transformation is a similarity transformation (i.e., fixes a given elliptic involution) that leaves the line at infinity pointwise invariant.^[2]

In Euclidean geometry, a homothety of ratio ${\displaystyle k}$ multiplies distances between points by ${\displaystyle |k|}$, areas by ${\displaystyle k^{2}}$ and volumes by ${\displaystyle |k|^{3}}$. Here ${\displaystyle k}$ is the ratio of magnification or dilation factor or scale factor or similitude ratio. Such a transformation can be called an enlargement if the scale factor exceeds 1. The above-mentioned fixed point S is called homothetic center or center of similarity or center of similitude.

The term, coined by French mathematician Michel Chasles, is derived from two Greek elements: the prefix homo- (όμο), meaning "similar", and thesis (Θέσις), meaning "position". It describes the relationship between two figures of the same shape and orientation. For example, two Russian dolls looking in the same direction can be considered homothetic.

Homotheties are used to scale the contents of computer screens; for example, smartphones, notebooks, and laptops.