Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Verteilungsfunktion

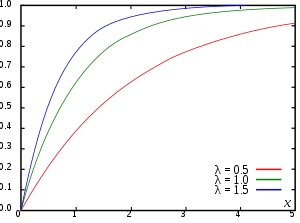
Die Verteilungsfunktion ist eine spezielle reelle Funktion in der Stochastik und ein zentrales Konzept bei der Untersuchung von Wahrscheinlichkeitsverteilungen auf den reellen Zahlen. Jeder Wahrscheinlichkeitsverteilung und jeder reellwertigen Zufallsvariable kann eine Verteilungsfunktion zugeordnet werden. Anschaulich entspricht dabei der Wert der Verteilungsfunktion an der Stelle der Wahrscheinlichkeit, dass die zugehörige Zufallsvariable einen Wert kleiner oder gleich annimmt. Ist beispielsweise die Verteilung der Schuhgrößen in Europa gegeben, so entspricht der Wert der entsprechenden Verteilungsfunktion bei 45 der Wahrscheinlichkeit, dass ein beliebiger Europäer die Schuhgröße 45 oder kleiner besitzt.
Ihre Bedeutung erhält die Verteilungsfunktion durch den Korrespondenzsatz, der besagt, dass jeder Verteilungsfunktion eine Wahrscheinlichkeitsverteilung auf den reellen Zahlen zugeordnet werden kann und umgekehrt. Die Zuordnung ist bijektiv. Dies ermöglicht es, anstelle der Untersuchung von Wahrscheinlichkeitsverteilungen als Mengenfunktionen auf einem komplexen Mengensystem mit Methoden der Maßtheorie die entsprechenden Verteilungsfunktionen zu untersuchen. Diese sind reelle Funktionen und somit über die Methoden der reellen Analysis leichter zugänglich.
Als alternative Bezeichnungen finden sich unter anderem kumulierte Verteilungsfunktion bzw. kumulative Verteilungsfunktion, da sie die Wahrscheinlichkeiten, kleiner als zu sein, anhäuft (siehe auch kumulierte Häufigkeit). Weiterhin wird sie zur besseren Abgrenzung von ihrem höherdimensionalen Pendant, der multivariaten Verteilungsfunktion, auch als univariate Verteilungsfunktion bezeichnet.[1] In Abgrenzung zum allgemeineren maßtheoretischen Konzept einer Verteilungsfunktion finden sich die Bezeichnungen als wahrscheinlichkeitstheoretische Verteilungsfunktion oder als Verteilungsfunktion im engeren Sinn.[2]
Die Entsprechung der Verteilungsfunktion in der deskriptiven Statistik ist die empirische Verteilungs- oder Summenhäufigkeitsfunktion.
Previous Page Next Page




