Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Superellipse
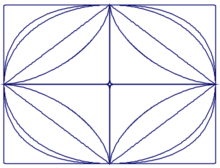
a = 1,0, b = 0,75
n = 0,15, 2/3, 1, 2, 2,5 og 500
En superellipse er en matematisk kurve som kan opfattes som mellemting mellem en ellipse og et rektangel. En superellipse kan i et kartesisk koordinatsystem beskrives som mængden af punkter (x, y) som opfylder ligningen
hvor n, a og b er reelle tal > 0.
a og b er figurens halvakser. Formlen er en generalisering af formlen for en ellipse hvor n = 2. For n større end 2 fås en superellipse, og for n mellem 0 og 2 fås en subellipse.
Kurverne blev først beskrevet af den franske fysiker og matematiker Gabriel Lamé (1795-1870), men de blev gjort kendte og navngivet superellipse af Piet Hein.
Byplanlæggere i Stockholm havde problemer med et rektangulært torv i byen, Sergels torg. Man ønskede en blød eller smidig kurve, som var en mellemting mellem det firkantede og cirklen. Piet Hein løste problemet ved at lave en superellipse med n = 2,5. Han brugte også superellipsen i arkitektur og møbeldesign.

Desuden opfandt Hein det såkaldte superæg, som er en tredimensionel superellipsoide (en superellipse med n = 2,5, a = 4 og b = 3 roteret omkring x-aksen):
Superægget kan i modsætning til en almindelig ellipsoide stå oprejst på en flad overflade idet dets krumningsradier i toppunkterne er uendelig store.
Previous Page Next Page




