Cerchio

Disambiguazione – Se stai cercando altri significati, vedi Cerchio (disambigua).

Disambiguazione – Se stai cercando cerchio inteso come linea circolare, vedi Circonferenza.

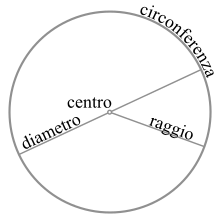
Il cerchio, geometria piana, è la parte di piano delimitata da una circonferenza^[1] ed è costituito dall'insieme infinito dei punti che distano da un punto dato, detto centro, non più di una distanza fissata detta raggio. In un sistema di assi un generico cerchio di centro ${\displaystyle (a;b)}$ e raggio ${\displaystyle r}$ è rappresentato dall'insieme di punti che soddisfano la seguente condizione:

${\displaystyle {\overline {D}}=\{(x,y)\in {\mathbb {R} ^{2}}:(x-a)^{2}+(y-b)^{2}\leq r^{2}\}.}$

Esso può essere immaginato come un poligono regolare con un numero di lati infinito, o meglio come il limite di una successione di poligoni regolari ad ${\displaystyle n}$ lati per ${\displaystyle n}$ che tende ad infinito. Il cerchio è una figura convessa.

Un segmento avente gli estremi sulla circonferenza è detto corda; ognuna delle due parti in cui questa divide il cerchio si chiama segmento circolare. Se la corda in questione passa per il centro, essa si chiama diametro e i due segmenti sono congruenti e si chiamano semicerchi.

Un segmento circolare può anche essere la parte di cerchio compresa tra due corde parallele.

L'intersezione fra un angolo al centro, cioè un angolo avente come vertice il centro del cerchio, ed il cerchio stesso (visivamente, uno "spicchio" di cerchio) si chiama settore circolare. Se l'angolo al centro è retto, il settore circolare che individua si chiama quadrante; se è piatto, è il semicerchio.

Due cerchi aventi lo stesso centro si dicono concentrici. L'area compresa fra le due circonferenze si chiama corona circolare.

La formula dell'area del cerchio può essere ottenuta come limite di quella del poligono regolare, ovvero come lunghezza della circonferenza per raggio diviso ${\displaystyle 2}$:

${\displaystyle \mathrm {Area} ={\frac {\mathrm {circonferenza} \times \mathrm {raggio} }{2}}=\pi r^{2}.}$

La quadratura del cerchio si riferisce all'impossibile compito di costruire con riga e compasso, a partire da un cerchio, un quadrato avente stessa area.

Alcuni solidi tridimensionali che possono avere, se tagliati da un piano, sezioni circolari sono la sfera, il cilindro ed il cono.

Il cerchio viene detto inscritto in un poligono quando la sua circonferenza è tangente ad ogni lato di quest'ultimo, e circoscritto quando i vertici di un poligono stanno sulla circonferenza.