Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Cumulative distribution function
This article needs additional citations for verification. (March 2010) |
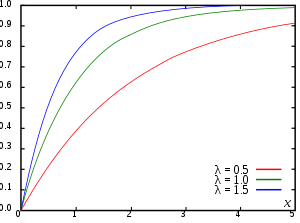
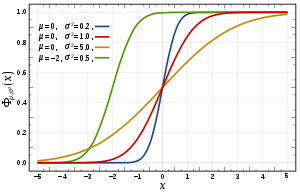
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable , or just distribution function of , evaluated at , is the probability that will take a value less than or equal to .[1]
Every probability distribution supported on the real numbers, discrete or "mixed" as well as continuous, is uniquely identified by a right-continuous monotone increasing function (a càdlàg function) satisfying and .
In the case of a scalar continuous distribution, it gives the area under the probability density function from negative infinity to . Cumulative distribution functions are also used to specify the distribution of multivariate random variables.
- ^ Deisenroth, Marc Peter; Faisal, A. Aldo; Ong, Cheng Soon (2020). Mathematics for Machine Learning. Cambridge University Press. p. 181. ISBN 9781108455145.
Previous Page Next Page



![{\displaystyle F\colon \mathbb {R} \rightarrow [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4c45b6faf38bb3fb300ab4678d3675afd172f56)



